OBJETIVO GENERAL:
El estudiante adquirirá destreza en el manejo de técnicas y procedimientos para la solución de problemas. Hará uso de lenguaje matemático, de la sistematización de información y de las formas de representación gráfica y analítica. Manejará los conocimientos, métodos y algoritmos matemáticos establecidos en los programas, tanto básicos como auxiliares para abordar los contenidos de otras materias. Elaborará y usará modelos matemáticos en la resolución de problemas de optimización de recursos.
Unidad I. Funciones.
Objetivo especifico:
El alumno entenderá el concepto de función y su manipulación algebraica, así como su representación gráfica. Resolverá problemas de aplicación, dando especial énfasis a aquellos relacionados con las áreas económico administrativas, tales como la Economía, Mercadotecnia, Administración, Turismo, Recursos Humanos, Sistemas de Información y Negocios Internacionales.
1.1 Definición y notación de función.
Definición de Función:
1.1 Definición y notación de función.
Definición de Función:
En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito).
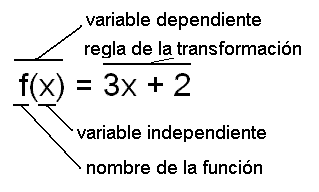
Notación de la función
| La notación de la función es una manera de
escribir funciones
que aclara el nombre de la función, de las variables independientes,
de las variables dependientes,
y de la regla de la transformación.
En el ejemplo, f(x) es la variable dependiente, f es el nombre de función, x es la variable independiente, y 3x + 2 es la regla de la transformación. |
1.2 Dominio y rango de una función.
*Valor de entrada se llama: "Dominio"
*Valor de salida se llama: "Rango" / "Codominio"
NOTA: Cuando las funciones son polinomios los dominios son todos reales.
- Dos
funciones iguales si,solo si el dominio de la primera es igual al
dominio de la segunda. " g(x) = f(x) <==> Dg(x) = Df(x)
- Para toda definición y notación de función x en el dominio de cada una de las funciones me da el mismo valor e salida (Rango).
g (x) = 2x +8
DG (x) = x E (-∞,∞)
g (1) = 2(1) +8 =10
1.3 Tipos de funciones.
Funciones Algebraicas
En las funciones algebraicas
las operaciones que hay que efectuar con la variable independiente son: la
adición, sustracción, multiplicación, división, potenciación y radicación.
Las funciones algebraicas
pueden ser:
Funciones explícita
Si se pueden obtener las
imágenes de x por simple sustitución.
f(x) = 5x − 2
Funciones implícita
Si no se pueden obtener las
imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.
5x − y − 2 = 0
Funciones polinómicas
Son las funciones que vienen
definidas por un polinomio.
f(x) = a0 + a1x + a2x² +
a2x³ +··· + anxn
Su dominio es R, es decir,
cualquier número real tiene imagen.
Funciones constantes
El criterio viene dado por
un número real.
f(x)= k
La gráfica es una recta horizontal paralela a al eje de abscisas
Función racional
El criterio viene dado por
un cociente entre polinomios:

El dominio lo forman todos
los números reales excepto los valores de x que anulan el denominador.
Función exponencial

Sea a un número real
positivo. La función que a cada número real x le hace corresponder la potencia a^x se llama
función exponencial de base a y exponente x.
Función logarítmica
La función logarítmica en
base a es la función inversa de la exponencial en base a.
1.4 Operaciones con funciones.
Álgebra de funciones
Suma, resta, multiplicación y división de funciones
Sean f y g dos funciones cualesquiera.
Se define 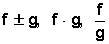 como
como
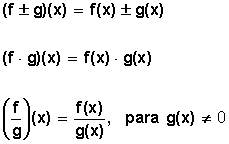
Ejemplos:
Suma de funciones
Sean las funciones
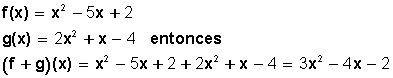
Resta de funciones
Producto de funciones
Sean las funciones
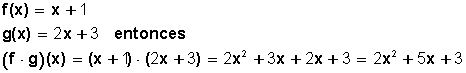
División de funciones
Sean las funciones
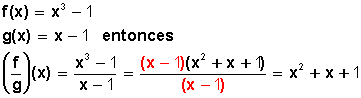
1.5 Composición de funciones.
1Sean las funciones:

1Calcular (f o g) (x)


2Calcular (g o f) (x)


2

1

2

3

1

2


1.6 Gráfica de una función.
En matemáticas, la gráfica de una función:
Es el conjunto formado por todos los pares ordenados (x, f(x)) de la función f, es decir, como un subconjunto del producto cartesianoX×Y. Se representa gráficamente mediante una correspondencia entre los elementos del conjunto dominio y los del conjunto imagen.
Las únicas funciones que se pueden trazar de forma completa son las de una sola variable, con un sistema de coordenadas cartesianas,
donde cada abscisa representa un valor de la variable del dominio y
cada ordenada representa el valor correspondiente del conjunto imagen.
Si la función es continua, entonces la gráfica formará una línea recta o curva.
En el caso de
funciones de dos variables es posible visualizarlas de forma unívoca
mediante una proyección geométrica, pero a partir de tres variables tan
solo es posible visualizar cortes (con un plano) de la función para los
que los valores de todas las variables, excepto dos, permanezcan
constantes.
1.7 Función lineal y función cuadrática.
-CUADRÁTICA:
Las ecuaciones cuadráticas o de segundo grado son las expresiones de la forma:
ax2 + bx +c = 0 con a ≠ 0
Para resolver ecuaciones de segundo grado utilizamos la siguiente fórmula:


-LINEAL:
-CUADRÁTICA:
Las ecuaciones cuadráticas o de segundo grado son las expresiones de la forma:
ax2 + bx +c = 0 con a ≠ 0
Para resolver ecuaciones de segundo grado utilizamos la siguiente fórmula:

-LINEAL:
Una
función lineal es una función cuyo dominio son todos los números
reales, cuyo codominio también todos los números reales, y cuya
expresión analítica es un polinomio de primer grado.
La función lineal se define por la ecuación f(x) = mx + b ó y = mx + b llamada ecuación canónica, en donde m es la pendiente de la recta y b es el intercepto con el eje Y.
Por ejemplo,
son funciones lineales f(x) = 3x + 2 g(x) = - x + 7 h(x) = 4 (en esta m
= 0 por lo que 0x no se pone en la ecuación).
Esta es la gráfica de la función lineal y = 3x + 2
Vemos que m = 3 y b = 2 (de la forma y = mx + b)
Este número m se
llama pendiente de la recta y es la relación entre la altura y
la base, aquí vemos que por cada unidad recorrida en x la recta sube 3
unidades en y por lo que la pendiente es m = 3. & b es el intercepto
de la recta con el eje Y (donde la recta se cruza con el eje Y)
1.8 Función exponencial y logarítmica.
1.9 Aplicaciones en las ciencias económico administrativas: funciones de oferta y demanda; recta presupuestal, funciones de ingresos, costos y utilidades; funciones de
apreciación y depreciación.
CRECIMIENTO POBLACIONAL:
FORMULA: M= c (1+i) n P=Po (1+i) t
Ejemplo: La población de una ciudad de 1000 habitantes crecen a razón de 2% anual.Encuentre la población de 3 años.
Po=10000
i=2%
t=3 años
P=10000 (1.02)³ =10612.
CONCLUSIÓN FINAL UNIDAD 1:
apreciación y depreciación.
CRECIMIENTO POBLACIONAL:
FORMULA: M= c (1+i) n P=Po (1+i) t
Ejemplo: La población de una ciudad de 1000 habitantes crecen a razón de 2% anual.Encuentre la población de 3 años.
Po=10000
i=2%
t=3 años
P=10000 (1.02)³ =10612.
CONCLUSIÓN FINAL UNIDAD 1:
Tras el
estudio de las funciones matemáticas, podemos concluir en que son muy
importantes tanto para las matemáticas como para muchas otras ciencias.
El objetivo
planteado en la introducción se cumplió, ya que se pudo observar a lo
largo del desarrollo del trabajo los diferentes usos de las funciones y,
al haber también estudiado las ecuaciones matemáticas, queda como un
modelo que podemos aplicar frente a cierta problemática
DERECHOS DE AUTOR UNIDAD 1:
http://www.profesorenlinea.com.mx/matematica/Funciones_matematicas.html
http://www.allmathwords.org/es/f/functionnotation.html
http://www.google.cl/search?q=+%22funci%C3%B3n+lineal+es%22&hl=es&lr=lang_es&ie=UTF-8&oe=UTF-8&as_qdr=all&start=30&sa=N
Objetivo: El
alumno comprenderá la noción de límite y de continuidad de una función; las
propiedades de los límites y los casos especiales de los límites. Aprenderá a
calcular el límite de una función.
Unidad II. Límites y continuidad.
2.1 Definición de límite.
El límite de una función es un concepto fundamental del análisis matemático, un caso de límite aplicado a las funciones.
Intuitivamente, el hecho que una función f alcance un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente próximos a c, sin importar el valor que pudiera adquirir o en el punto c.
http://es.wikipedia.org/wiki/L%C3%ADmite_de_una_funci%C3%B3n
http://definicion.de/limite-de-una-function
2.2. Propiedades de los limites
Los límites forman una parte fundamental del cálculo en
las Matemáticas. De hecho, el primer punto en el concepto del cálculo está
marcado por los límites. Los límites pueden ser entendidos fácilmente al
observar sus propiedades.
Las Propiedades de los límites implican operaciones que
se pueden emplear con el fin de simplificar el límite de una función y
convertirlos en una forma mucho más sencilla. Estas propiedades pueden
utilizarse con el fin de encontrar los límites de las combinaciones de dos o
más funciones o para demostrar si el límite de la función existe o no.
Cuando se trata con la combinación de dos o más
funciones, por lo general, los límites de las funciones se calculan individualmente,
con la ayuda de estas propiedades, y por último combinando estos con el fin de
llegar al resultado final.
Estas propiedades expresan que el resultado será el mismo
si el límite es tomado primero y después se realiza el álgebra o realizando el
álgebra primero y luego tomando los límites.
Las propiedades de los límites, también
conocidas como “Teoremas De Límite
Central “, se pueden establecer como:
1). El límite de una función siempre es único y es por
esta razón que siempre se refiere a estos como “El Límite” y no simplemente
límite. Esta propiedad básica se puede demostrar como:
Si  y,
y,  Entonces, L1 = L2
Entonces, L1 = L2
2). El límite de la sumatoria de dos funciones es igual a
la suma de los límites de las dos funciones por separado.
3). Del mismo modo, el límite de la resta de dos
funciones es igual a la resta de los límites de las dos funciones por separado.
4). El caso similar se puede demostrar con la
multiplicación, es decir,
5). Para la división, la regla básica es similar a la de
la suma y la resta. Sin embargo, en el caso de la división, , esto es, se debe
tener cuidado para que el denominador no se convierta en 0 ya que dará lugar a
un “error cero”.
6). Una constante que se multiplica con el límite, se
puede tomar fuera del límite sin afectar el resultado. Es decir,
7). El límite de un número fijo o inmutable es un número
fijo en sí mismo.
8). El límite global de la proporción (cociente) de dos
funciones es la proporción del límite de las dos funciones por separado.
9). Límite de la Función Exponencial: De acuerdo a esta
propiedad,
10). Límite de una Función Logarítmica: De acuerdo a
ella,
11). Teorema de Estricción: Considerando el caso f® g® h®
para r acercarse a x .Si
2.3 Límites laterales.
El concepto de límite está íntimamente ligado al concepto de función. Cada uno de los números que se acerca a 4 pueden obtenerse de una ecuación (lineal por ejemplo) como y = 4 + x. Donde al darle valores a x obtenemos
"esos" números que se acercan a 4 por derecha e izquierda.
Evidentemente, de acuerdo al tipo de ecuación que tengamos, serán los
valores de x a tomar en cuenta.
En este caso no nos interesa cuando x = 0, ya que no queremos que "la cuenta" de 4 (que es nuestro límite).
x
y = 4 + x
– 0,1 3,9 – 0,01 3,99 – 0,001 3,999 – 0,0001 3,9999
¬ Por izquierda
Por derecha ®
x
y = 4 + x
0,1
4,1
0,01 4,01 0,001 4,001 0,0001 4,0001
El valor de x se acerca a "cero" y el valor de "y" (la imagen de la función) se acerca a 4. Para hablar con propiedad, en matemática no se dice "se acerca a" sino "tiende a"; x tiende a cero cuando y tiende
a cuatro. Es real, a los que hacemos matemática no nos gusta escribir
mucho. Se reemplaza las palabras con símbolos para ahorrar tiempo (el
esfuerzo mental se reserva para el problema matemático). Así que en vez
de escribir "tiende a" se pone una flecha. De manera que "x tiende a cero" se indica "x ® 0" e "y tiende a cuatro" se escribe como "y ® 4".
Ya estamos
un poco más cerca de poder leer "matemáticamente". El límite (lím) suele
escribirse indicando debajo de él el valor a que tiende x, seguido de la ecuación que se analiza y (después del igual) se indica el valor del límite.


2.3 Límites laterales.
El concepto de límite está íntimamente ligado al concepto de función. Cada uno de los números que se acerca a 4 pueden obtenerse de una ecuación (lineal por ejemplo) como y = 4 + x. Donde al darle valores a x obtenemos
"esos" números que se acercan a 4 por derecha e izquierda.
Evidentemente, de acuerdo al tipo de ecuación que tengamos, serán los
valores de x a tomar en cuenta.
En este caso no nos interesa cuando x = 0, ya que no queremos que "la cuenta" de 4 (que es nuestro límite).
| ¬ Por izquierda Por derecha ® |
|
El valor de x se acerca a "cero" y el valor de "y" (la imagen de la función) se acerca a 4. Para hablar con propiedad, en matemática no se dice "se acerca a" sino "tiende a"; x tiende a cero cuando y tiende
a cuatro. Es real, a los que hacemos matemática no nos gusta escribir
mucho. Se reemplaza las palabras con símbolos para ahorrar tiempo (el
esfuerzo mental se reserva para el problema matemático). Así que en vez
de escribir "tiende a" se pone una flecha. De manera que "x tiende a cero" se indica "x ® 0" e "y tiende a cuatro" se escribe como "y ® 4".
Ya estamos
un poco más cerca de poder leer "matemáticamente". El límite (lím) suele
escribirse indicando debajo de él el valor a que tiende x, seguido de la ecuación que se analiza y (después del igual) se indica el valor del límite.


2.4. Límites al infinito.
Una función f(x) tiene por límite +∞ cuando x → a, si fijado un número real positivo K > 0 se verifica que f(x) > k para todos los valores próximos a a.
Ejemplo
2.5. Continuidad y discontinuidad.
Condiciones
que debe cumplir una función para que sea continúa en un punto. Si alguna
condición no se cumple la función presentara una discontinuidad en ese punto.


2.6. Aplicaciones a las ciencias económico administrativas: interés compuesto continuamente, límite de la función costo promedio.
El interés
compuesto representa el costo del dinero, beneficio o utilidad de
un capital inicial (C) o principal a una tasa de interés (i) durante
un período (t), en el cual los intereses que se obtienen al final de
cada período de inversión no se retiran sino que se reinvierten o añaden
al capital inicial; es decir, se capitalizan, produciendo un capital
final (Cf).
Para un período determinado sería
Capital final (Cf) = capital inicial (C) más los intereses.
Veamos si podemos generalizarlo con un ejemplo:
Hagamos
cálculos para saber el monto final de un depósito inicial de $
1.000.000, a 5 años plazo con un interés compuesto de 10 % (como no se
especifica, se subentiende que es 10 % anual).
| Año |
Depósito inicial
|
Interés
|
Saldo final
|
0 (inicio)
|
$1.000.000
|
($1.000.000 x 10% = ) $100.000
|
$1.100.000
|
1
|
$1.100.000
|
($1.100.000 × 10% = ) $110.000
|
$1.210.000
|
2
|
$1.210.000
|
($1.210.000× 10% = ) $121.000
|
$1.331.000
|
3
|
$1.331.000
|
($1.331.000 × 10% = ) $133.100
|
$1.464.100
|
4
|
$1.464.100
|
($1.464.100 × 10% = ) $146.410
|
$1.610.510
|
5
|
$1.610.510
|
Paso a paso
resulta fácil calcular el interés sobre el depósito inicial y sumarlo
para que esa suma sea el nuevo depósito inicial al empezar el segundo
año, y así sucesivamente hasta llegar al monto final.
Resulta simple, pero hay muchos cálculos; para evitarlos usaremos una fórmula de tipo general:
En inversiones a interés compuesto, el capital final (Cf), que se obtiene a partir de un capital inicial (C), a una tasa de interés (i), en un tiempo (t), está dado por la fórmula:
Recordemos que i se expresa en forma decimal ya que corresponde a .
.
Y donde t corresponde al número de años durante los cuales se mantiene el depósito o se paga una deuda.
Y donde t corresponde al número de años durante los cuales se mantiene el depósito o se paga una deuda.
Como corolario a esta fórmula:
A partir de
ella, puesto que el interés compuesto final (I) es la diferencia entre
el capital final y el inicial, podríamos calcular la tasa de interés
(i):
Sacamos factor común C:
También podemos calcular la tasa de interés despejando en la fórmula de Cf:

En los
problemas de interés compuesto i y t deben expresarse en la misma unidad
de tiempo efectuando las conversiones apropiadas cuando estas variables
correspondan a diferentes períodos de tiempo.
EJEMPLO:
Averiguar en qué se convierte un capital de 1.200.000 pesos al cabo de 5 años, y a una tasa de interés compuesto anual del 8 %.
Resolución:
Aplicando la fórmula
Resolución:
Aplicando la fórmula
Reemplazamos con los valores conocidos:
En tasa de interés compuesto 
Capital inicial 
Tiempo en años (t) = 5

Respuesta:
El capital final es de 1.763.194 pesos.
Leer más: http://www.monografias.com/trabajos41/derivada-y-limite/derivada-y-limite2.shtml#ixzz3b0Iq7HFr
Conclusión Unidad 2:
El límite es el comportamiento de dicha función en el entorno de un punto, sin
importar qué sucede en el mismo (puede incluso no estar definida la función en dicho
sitio). Al igual si una función es continua, entonces sus límites por la
derecha y por la izquierda son los mismos. Si el límite no existe,
entonces tenemos una discontinuidad esencial.
Unidad 3. Derivada de una función
OBJETIVO:
El alumno entenderá el concepto de derivada y su interpretación geométrica y como razón de cambio.
Utilizará la definición de la derivada para obtener algunas reglas de derivación.
Aplicará las reglas de derivación en la resolución de problemas que involucren los conceptos de tasa instantánea de cambio, tangente a una curva en un punto; y medida marginal de funciones de costo, utilidad, ingreso y producción.
3.1. Definición de la derivada.
La derivada
de una función es una
medida de la rapidez con la que cambia el valor de dicha función matemática,
según cambie el valor de su variable
independiente. La derivada de una función es un concepto local, es
decir, se calcula como el límite de la rapidez
de cambio media de la función en un cierto intervalo, cuando el intervalo
considerado para la variable independiente se torna cada vez más pequeño. Por
ello se habla del valor de la derivada de una cierta función en un punto
dado.
Entonces el valor
de la derivada de una función en un punto puede interpretarse geométricamente,
ya que se corresponde con la pendiente de la recta tangente a la gráfica de la función en
dicho punto. La recta tangente es a su vez la gráfica de la mejor aproximación
lineal de la función alrededor de dicho punto.
La noción de
derivada puede generalizarse para el caso de funciones de más de una variable
con la derivada
parcial y el diferencial.

La derivada de la función en el punto marcado equivale a
la pendiente de la recta tangente (la gráfica de la función está dibujada en
rojo; la tangente a la curva está dibujada en verde).
http://es.wikipedia.org/wiki/Derivada
http://definicion.de/derivada/
3.2 Diferenciación de funciones por incrementos.
La derivada de una función f esla función denotada por f' (f prima) y definida por
f' (x) = lim f(z)-f(x) lim f(x+h) -f(x)
z-->x ------------ = h-->0 --------------
z-x h
siempre que este límite exista.Si
f' (a) puede encontrarse se dice que f esdiferenciable en a y f' (a) se
llama derivada de f(a),o derivada de f con respecto a x en a. El
proceso de encontrar la derivada se llama diferenciación.


NOTA : Si f es diferenciable en a, entonces f es continua en a.
REGLAS PARA LA DIFERENCIACION:
1) d
---- (c) = 0 la derivada de una constante es 0.
dx
2) d
----- (xn) = nxn-¹
dx
3) d
----- (cxn) = cn x n-¹
dx
4) d d d
----- (f(x) + g(x) ) = ------- f(x) ------ g(x)
dx dx dx
3.3 La derivada como razón de cambio.
Derivada = f'
Sea u y v una función derivable entonces la derivada de u por v es la del producto, es igual a la uv' mas la v'u.
(uv) = u'v +v'u
EJEMPLO: f(x) = (3x² +5) ( 4x² +6)
u= 3x² u'= 6x
v0 4x² +6 v' =8x
f'(x) = 6x (4x²+6) + 8x (3x² +5)
= 24x³ +36x +24x³ +40x
= f' (x) = 48x³ + 76x
3.4 Diferenciabilidad y continuidad.
Así como existen límites
unilaterales también podemos hablar de derivadas unilaterales. A
continuación se dan las definiciones de derivadas por la derecha y por
la izquierda de una función en un punto determinado.
v La
continuidad de una función en un número no implica que la función sea
derivable en dicho número; por ejemplo, la función valor absoluto es
continua en 0 pero no es diferenciable en cero. Veamos:



3.5 Reglas básicas de derivación:
Una función de grado n, donde n es un exponente real, se representa por 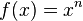 y su derivada es
y su derivada es  .
.
Algunos tipos de este tipo de funciones son: Función cuadrática, función cúbica, entre otras.
Por ejemplo la función:

Lo primero es "bajar" el exponente de
tal forma que éste multiplique a la variable con respecto a la cual
estamos derivando, luego al mismo exponente se le resta la unidad
formando uno nuevo, así:
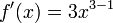
Quedando finalmente:
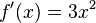
Cuando una función esté representada por medio de 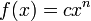 , su derivada equivale a
, su derivada equivale a  de la siguiente manera:
de la siguiente manera:
Consideremos la siguiente función: 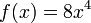 ,
lo primero a hacer es "bajar" al exponente a multiplicar por la
variable y el coeficiente que la acompaña, y de nuevo se halla un nuevo
exponente de la misma manera explicada anteriormente:
,
lo primero a hacer es "bajar" al exponente a multiplicar por la
variable y el coeficiente que la acompaña, y de nuevo se halla un nuevo
exponente de la misma manera explicada anteriormente:

Para obtener
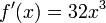
Cuando una constante acompaña a una variable cuyo exponente es 1 su derivada será el valor de la constante:
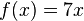
Entonces su derivada con respecto a esta variable será:
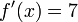
Puesto que 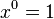
Considérese la función 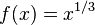
Se tiene:
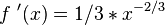
-
Se puede demostrar a partir de la definición de derivada, que la
derivada de la suma de dos funciones es la suma de las derivadas de cada
una.
Es decir,
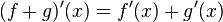 o
o ![\frac{d[f(x)+g(x)]}{dx}=\frac{df}{dx}+\frac{dg}{dx}](http://upload.wikimedia.org/math/7/1/5/7151a57c6b721f3f59162f9cf4db47d6.png) .
Como ejemplo consideremos la función
.
Como ejemplo consideremos la función  , para determinar su derivada se trabaja la derivada de cada término aparte y la suma de ambos será la derivada de la función:
, para determinar su derivada se trabaja la derivada de cada término aparte y la suma de ambos será la derivada de la función:
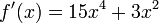
-
La derivada se expresa literalmente de la siguiente forma:
"La derivada de un producto de dos funciones es equivalente a la suma
entre el producto de la primera función sin derivar y la derivada de la
segunda función y el producto de la derivada de la primera función por
la segunda función sin derivar."
Y matemáticamente expresado por la relación
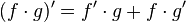 . Consideremos la siguiente función como ejemplo:
. Consideremos la siguiente función como ejemplo:
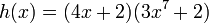 Identificamos a
Identificamos a  y
y 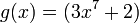 , utilizando las reglas anteriormente expuestas, vemos que:
, utilizando las reglas anteriormente expuestas, vemos que:
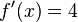 y que
y que 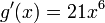 Por lo tanto
Por lo tanto
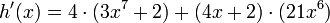 Simplificando y organizando el producto obtenido nos queda:
Simplificando y organizando el producto obtenido nos queda:
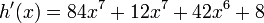 Sumamos términos semejantes y finalmente obtenemos la derivada:
Sumamos términos semejantes y finalmente obtenemos la derivada:
 Si por ejemplo tenemos la derivada del producto de tres funciones que
dependen de la misma variable, podemos pensar el producto de dos de las
funciones como si se tratara de una tercera función es decir
Si por ejemplo tenemos la derivada del producto de tres funciones que
dependen de la misma variable, podemos pensar el producto de dos de las
funciones como si se tratara de una tercera función es decir 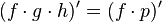 en donde
en donde 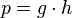 (sin importar que dos funciones escogemos).
(sin importar que dos funciones escogemos).
-
La derivada de un cociente se determina por la siguiente relación:
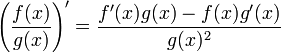
Para aquellos que se puedan confundir por algunas variables de más se puede escribir así:
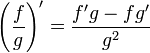
Es decir:
"La derivada de un cociente de dos funciones es la función ubicada en el
denominador por la derivada del numerador menos la derivada de la
función en el denominador por la función del numerador sin derivar, todo
sobre la función del denominador al cuadrado".
Este caso se relaciona mucho con la regla de derivada de un producto,
pero hay que tener en cuenta la resta y el orden de los factores. Pero
ya explicando lo dicho anteriormente consideremos como ejemplo la
siguiente función:

Ahora se trabaja el enunciado anterior el cual nos dice que multipliquemos el denominador que en este caso es  y se multiplique por la derivada del numerador que seria
y se multiplique por la derivada del numerador que seria 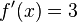 ; luego la segunda parte dice que tomemos la función del numerador (
; luego la segunda parte dice que tomemos la función del numerador ( ) sin derivar y lo multipliquemos por la derivada de
) sin derivar y lo multipliquemos por la derivada de  , que seria
, que seria 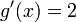 , todo esto lo dividimos entre el denominador al cuadrado, así:
, todo esto lo dividimos entre el denominador al cuadrado, así:

Ahora todo es cuestión de simplificar:
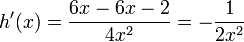
-
-
3.6 La regla de la cadena y de la potencia.
-
En términos intuitivos, si una variable y, depende de una segunda variable u, que a la vez depende de una tercera variable x; entonces, la razón de cambio de y con respecto ax puede ser calculada con el producto de la razón de cambio de y con respecto a u multiplicado por la razón de cambio de u con respecto a x.
Descripción algebraica
En términos algebraicos, la regla de la cadena (para funciones de una variable) afirma que si  es diferenciable en
es diferenciable en  y
y  es una función diferenciable en
es una función diferenciable en  , entonces la función compuesta
, entonces la función compuesta 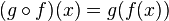 es diferenciable en
es diferenciable en  y
y

Notación de Leibniz
Alternativamente, en la notación de Leibniz, la regla de la cadena puede expresarse como:

donde  indica que g depende de f como si ésta fuera una variable.
indica que g depende de f como si ésta fuera una variable.
-
Regla de la potencia
3.7. Aplicaciones a las
ciencias económico administrativas: costo marginal, ingreso marginal, utilidad
marginal, propensión marginal al consumo y propensión marginal al ahorro.
El
costo marginal se define como la
variación en el costo total, ante el aumento de una unidad en la cantidad
producida, es decir, es el costo de producir una unidad adicional.
Matemáticamente se expresa como la derivada parcial del
costo total respecto a la cantidad:
Costo Marginal = ∂Costo Total / ∂Cantidad
CMg = ∂CT / ∂Q
El costo marginal es un concepto fundamental en la teoría
microeconómica, debido a que se
utiliza para determinar la cantidad de producción de las empresas y los precios
de los productos.
El costo marginal depende de la tecnología utilizada en
la producción y de los precios de los insumos y los factores de producción.
Siguiendo la teoría
neoclásica, el gráfico del costo marginal en el corto plazo tiene
forma de U debido a que para pocas unidades producidas se tiene mucho capital
(insumos fijos) y pocos trabajadores (insumos variables), por lo que los
primeros trabajadores aumentan mucho la producción debido a que tienen mucho
capital disponible. A medida que se van agregando trabajadores, la producción
sigue aumentando pero cada vez menos, porque el capital se mantiene fijo.
El ingreso marginal está íntimamente
relacionado con el costo marginal y su
función. Así el ingreso marginal será la inversa a la anterior.
Si el precio de
venta es fijo, el ingreso marginal será creciente mientras el costo marginal sea
decreciente y será decreciente cuando el anterior sea creciente ya que el
ingreso marginal se calcula restando al precio el costo marginal de esa
nueva unidad vendida. Estos cálculos son válidos siempre que el precio sea
constante en un mercado de competencia perfecta,
regulado por la teoría de la oferta y la demanda, para
aumentar la cantidad vendida debe reducirse el precio de toda la producción por
lo que el dato de ingreso marginal es anecdótico.
Utilidad
Marginal es el aumento o disminución de la utilidad total que acompaña el aumento o
disminución de la cantidad que se posee de un Bien. Un ejemplo que lo ilustra es el caso de ua persona sedienta que
encuentra un vaso de agua en el desierto. El primer vaso será extremadamente
valorado. Pero si se toma un segundo vaso dicha valoración va a ser menor. El vaso numero 10 probablemente no le generará ningún placer, pudiendo ocasionar incluso un malestar.
La propensión marginal al consumo se define como el aumento del consumo con la renta disponible, matemáticamente puede
expresarse como la siguiente derivada:

Que explica cuánto varía el consumo cuando varía el
ingreso. En el análisis de consumo keynesiano, se formula la siguiente expresión de consumo:

Que se considera aproximadamente válida para intervalos
de variación de la renta en los que la PMC permanece aproximadamente constante:
 = Consumo
= Consumo
 = Consumo autónomo o fijo.
= Consumo autónomo o fijo.
 = Propensión marginal a consumir
= Propensión marginal a consumir
 = Ingreso disponible
= Ingreso disponible 
 = Propensión marginal a ahorrar.
= Propensión marginal a ahorrar.
La propensión
marginal al ahorro se define partir de la propensión
marginal a consumir. Matemáticamente puede expresarse como la siguiente
derivada:

que explica cuánto varía el consumo cuando varía el
ingreso. En el análisis de consumo keynesianismo, se formula la
siguiente expresión de consumo:

Que se considera aproximademente válida para intervalos
de variación de la renta en los que la PMC permanece aproximadamente constante:
 = Consumo
= Consumo
 = Consumo
autónomo o fijo.
= Consumo
autónomo o fijo.
 = Propensión
marginal al consumo
= Propensión
marginal al consumo
 = Ingreso
disponible
= Ingreso
disponible 
 = Propensión
marginal a ahorrar.
= Propensión
marginal a ahorrar.
Conclusión Unidad 3:
La importancia que tiene al estudiar
derivados y límites, nos permite conocer cómo se ejecuta todos sus pasos; La derivada se aplica en los casos donde es necesario medir
la rapidez con que se produce el cambio de una situación. La derivación
constituye una de las operaciones de mayor importancia cuando tratamos de
funciones reales de variable real puesto que nos indica la tasa de variación de
la función en un instante determinado o para un valor determinado de la
variable, si ésta no es el tiempo. Al igual, la derivada de una función para un
valor de la variable es la tasa de variación instantánea de dicha función y
para el valor concreto de la variable.
Conclusión Unidad 2:
El límite es el comportamiento de dicha función en el entorno de un punto, sin
importar qué sucede en el mismo (puede incluso no estar definida la función en dicho
sitio). Al igual si una función es continua, entonces sus límites por la
derecha y por la izquierda son los mismos. Si el límite no existe,
entonces tenemos una discontinuidad esencial.
3.1. Definición de la derivada.

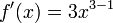
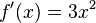

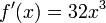
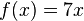
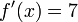
Unidad 3. Derivada de una función
OBJETIVO:
El alumno entenderá el concepto de derivada y su interpretación geométrica y como razón de cambio.
Utilizará la definición de la derivada para obtener algunas reglas de derivación.
Aplicará las reglas de derivación en la resolución de problemas que involucren los conceptos de tasa instantánea de cambio, tangente a una curva en un punto; y medida marginal de funciones de costo, utilidad, ingreso y producción.
3.1. Definición de la derivada.
La derivada
de una función es una
medida de la rapidez con la que cambia el valor de dicha función matemática,
según cambie el valor de su variable
independiente. La derivada de una función es un concepto local, es
decir, se calcula como el límite de la rapidez
de cambio media de la función en un cierto intervalo, cuando el intervalo
considerado para la variable independiente se torna cada vez más pequeño. Por
ello se habla del valor de la derivada de una cierta función en un punto
dado.
Entonces el valor
de la derivada de una función en un punto puede interpretarse geométricamente,
ya que se corresponde con la pendiente de la recta tangente a la gráfica de la función en
dicho punto. La recta tangente es a su vez la gráfica de la mejor aproximación
lineal de la función alrededor de dicho punto.
La noción de
derivada puede generalizarse para el caso de funciones de más de una variable
con la derivada
parcial y el diferencial.
La derivada de la función en el punto marcado equivale a la pendiente de la recta tangente (la gráfica de la función está dibujada en rojo; la tangente a la curva está dibujada en verde).
http://es.wikipedia.org/wiki/Derivada
http://definicion.de/derivada/
3.2 Diferenciación de funciones por incrementos.
La derivada de una función f esla función denotada por f' (f prima) y definida por
f' (x) = lim f(z)-f(x) lim f(x+h) -f(x)
z-->x ------------ = h-->0 --------------
z-x h
siempre que este límite exista.Si
f' (a) puede encontrarse se dice que f esdiferenciable en a y f' (a) se
llama derivada de f(a),o derivada de f con respecto a x en a. El
proceso de encontrar la derivada se llama diferenciación.


NOTA : Si f es diferenciable en a, entonces f es continua en a.
REGLAS PARA LA DIFERENCIACION:
1) d
---- (c) = 0 la derivada de una constante es 0.
dx
2) d
----- (xn) = nxn-¹
dx
3) d
----- (cxn) = cn x n-¹
dx
4) d d d
----- (f(x) + g(x) ) = ------- f(x) ------ g(x)
dx dx dx
3.3 La derivada como razón de cambio.
La derivada de una función f esla función denotada por f' (f prima) y definida por
f' (x) = lim f(z)-f(x) lim f(x+h) -f(x)
z-->x ------------ = h-->0 --------------
z-x h
siempre que este límite exista.Si f' (a) puede encontrarse se dice que f esdiferenciable en a y f' (a) se llama derivada de f(a),o derivada de f con respecto a x en a. El proceso de encontrar la derivada se llama diferenciación.


NOTA : Si f es diferenciable en a, entonces f es continua en a.
REGLAS PARA LA DIFERENCIACION:
1) d
---- (c) = 0 la derivada de una constante es 0.
dx
2) d
----- (xn) = nxn-¹
dx
3) d
----- (cxn) = cn x n-¹
dx
4) d d d
----- (f(x) + g(x) ) = ------- f(x) ------ g(x)
dx dx dx
3.3 La derivada como razón de cambio.
Derivada = f'
Sea u y v una función derivable entonces la derivada de u por v es la del producto, es igual a la uv' mas la v'u.
(uv) = u'v +v'u
EJEMPLO: f(x) = (3x² +5) ( 4x² +6)
u= 3x² u'= 6x
v0 4x² +6 v' =8x
f'(x) = 6x (4x²+6) + 8x (3x² +5)
= 24x³ +36x +24x³ +40x
= f' (x) = 48x³ + 76x
3.4 Diferenciabilidad y continuidad.
Así como existen límites
unilaterales también podemos hablar de derivadas unilaterales. A
continuación se dan las definiciones de derivadas por la derecha y por
la izquierda de una función en un punto determinado.
v La
continuidad de una función en un número no implica que la función sea
derivable en dicho número; por ejemplo, la función valor absoluto es
continua en 0 pero no es diferenciable en cero. Veamos:
 |  |
 | |
3.5 Reglas básicas de derivación:
Una función de grado n, donde n es un exponente real, se representa por 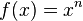 y su derivada es
y su derivada es  .
.
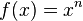 y su derivada es
y su derivada es  .
.
Algunos tipos de este tipo de funciones son: Función cuadrática, función cúbica, entre otras.
Por ejemplo la función:

Lo primero es "bajar" el exponente de
tal forma que éste multiplique a la variable con respecto a la cual
estamos derivando, luego al mismo exponente se le resta la unidad
formando uno nuevo, así:
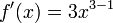
Quedando finalmente:
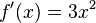
Cuando una función esté representada por medio de 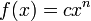 , su derivada equivale a
, su derivada equivale a  de la siguiente manera:
de la siguiente manera:
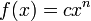 , su derivada equivale a
, su derivada equivale a  de la siguiente manera:
de la siguiente manera:
Consideremos la siguiente función: 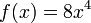 ,
lo primero a hacer es "bajar" al exponente a multiplicar por la
variable y el coeficiente que la acompaña, y de nuevo se halla un nuevo
exponente de la misma manera explicada anteriormente:
,
lo primero a hacer es "bajar" al exponente a multiplicar por la
variable y el coeficiente que la acompaña, y de nuevo se halla un nuevo
exponente de la misma manera explicada anteriormente:
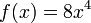 ,
lo primero a hacer es "bajar" al exponente a multiplicar por la
variable y el coeficiente que la acompaña, y de nuevo se halla un nuevo
exponente de la misma manera explicada anteriormente:
,
lo primero a hacer es "bajar" al exponente a multiplicar por la
variable y el coeficiente que la acompaña, y de nuevo se halla un nuevo
exponente de la misma manera explicada anteriormente:
Para obtener
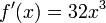
Cuando una constante acompaña a una variable cuyo exponente es 1 su derivada será el valor de la constante:
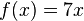
Entonces su derivada con respecto a esta variable será:
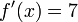
Puesto que 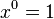
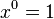
Considérese la función 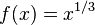
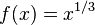
Se tiene:
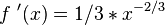
- Se puede demostrar a partir de la definición de derivada, que la derivada de la suma de dos funciones es la suma de las derivadas de cada una.Es decir,
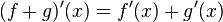 o
o ![\frac{d[f(x)+g(x)]}{dx}=\frac{df}{dx}+\frac{dg}{dx}](http://upload.wikimedia.org/math/7/1/5/7151a57c6b721f3f59162f9cf4db47d6.png) .Como ejemplo consideremos la función
.Como ejemplo consideremos la función , para determinar su derivada se trabaja la derivada de cada término aparte y la suma de ambos será la derivada de la función:
, para determinar su derivada se trabaja la derivada de cada término aparte y la suma de ambos será la derivada de la función: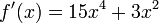
- La derivada se expresa literalmente de la siguiente forma:"La derivada de un producto de dos funciones es equivalente a la suma entre el producto de la primera función sin derivar y la derivada de la segunda función y el producto de la derivada de la primera función por la segunda función sin derivar."Y matemáticamente expresado por la relación
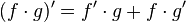 . Consideremos la siguiente función como ejemplo:
. Consideremos la siguiente función como ejemplo: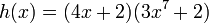 Identificamos a
Identificamos a y
y 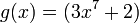 , utilizando las reglas anteriormente expuestas, vemos que:
, utilizando las reglas anteriormente expuestas, vemos que: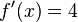 y que
y que 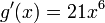 Por lo tanto
Por lo tanto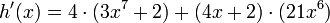 Simplificando y organizando el producto obtenido nos queda:
Simplificando y organizando el producto obtenido nos queda: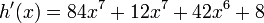 Sumamos términos semejantes y finalmente obtenemos la derivada:
Sumamos términos semejantes y finalmente obtenemos la derivada: Si por ejemplo tenemos la derivada del producto de tres funciones que dependen de la misma variable, podemos pensar el producto de dos de las funciones como si se tratara de una tercera función es decir
Si por ejemplo tenemos la derivada del producto de tres funciones que dependen de la misma variable, podemos pensar el producto de dos de las funciones como si se tratara de una tercera función es decir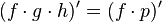 en donde
en donde 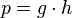 (sin importar que dos funciones escogemos).
(sin importar que dos funciones escogemos). - La derivada de un cociente se determina por la siguiente relación:
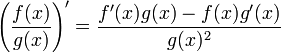
Para aquellos que se puedan confundir por algunas variables de más se puede escribir así:
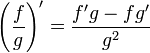
Es decir:
"La derivada de un cociente de dos funciones es la función ubicada en el denominador por la derivada del numerador menos la derivada de la función en el denominador por la función del numerador sin derivar, todo sobre la función del denominador al cuadrado".
Este caso se relaciona mucho con la regla de derivada de un producto, pero hay que tener en cuenta la resta y el orden de los factores. Pero ya explicando lo dicho anteriormente consideremos como ejemplo la siguiente función:

Ahora se trabaja el enunciado anterior el cual nos dice que multipliquemos el denominador que en este caso es y se multiplique por la derivada del numerador que seria
y se multiplique por la derivada del numerador que seria 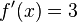 ; luego la segunda parte dice que tomemos la función del numerador (
; luego la segunda parte dice que tomemos la función del numerador ( ) sin derivar y lo multipliquemos por la derivada de
) sin derivar y lo multipliquemos por la derivada de  , que seria
, que seria 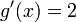 , todo esto lo dividimos entre el denominador al cuadrado, así:
, todo esto lo dividimos entre el denominador al cuadrado, así:

Ahora todo es cuestión de simplificar: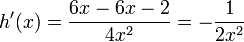
-
- 3.6 La regla de la cadena y de la potencia.
- En términos intuitivos, si una variable y, depende de una segunda variable u, que a la vez depende de una tercera variable x; entonces, la razón de cambio de y con respecto ax puede ser calculada con el producto de la razón de cambio de y con respecto a u multiplicado por la razón de cambio de u con respecto a x.
Descripción algebraica
En términos algebraicos, la regla de la cadena (para funciones de una variable) afirma que si es diferenciable en
es diferenciable en  y
y  es una función diferenciable en
es una función diferenciable en  , entonces la función compuesta
, entonces la función compuesta 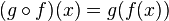 es diferenciable en
es diferenciable en  y
y
Notación de Leibniz
Alternativamente, en la notación de Leibniz, la regla de la cadena puede expresarse como:
donde indica que g depende de f como si ésta fuera una variable.
indica que g depende de f como si ésta fuera una variable. -
Regla de la potencia
3.7. Aplicaciones a las ciencias económico administrativas: costo marginal, ingreso marginal, utilidad marginal, propensión marginal al consumo y propensión marginal al ahorro.
El costo marginal se define como la variación en el costo total, ante el aumento de una unidad en la cantidad producida, es decir, es el costo de producir una unidad adicional.Matemáticamente se expresa como la derivada parcial del costo total respecto a la cantidad:Costo Marginal = ∂Costo Total / ∂CantidadCMg = ∂CT / ∂QEl costo marginal es un concepto fundamental en la teoría microeconómica, debido a que se utiliza para determinar la cantidad de producción de las empresas y los precios de los productos.El costo marginal depende de la tecnología utilizada en la producción y de los precios de los insumos y los factores de producción.Siguiendo la teoría neoclásica, el gráfico del costo marginal en el corto plazo tiene forma de U debido a que para pocas unidades producidas se tiene mucho capital (insumos fijos) y pocos trabajadores (insumos variables), por lo que los primeros trabajadores aumentan mucho la producción debido a que tienen mucho capital disponible. A medida que se van agregando trabajadores, la producción sigue aumentando pero cada vez menos, porque el capital se mantiene fijo.El ingreso marginal está íntimamente relacionado con el costo marginal y su función. Así el ingreso marginal será la inversa a la anterior.Si el precio de venta es fijo, el ingreso marginal será creciente mientras el costo marginal sea decreciente y será decreciente cuando el anterior sea creciente ya que el ingreso marginal se calcula restando al precio el costo marginal de esa nueva unidad vendida. Estos cálculos son válidos siempre que el precio sea constante en un mercado de competencia perfecta, regulado por la teoría de la oferta y la demanda, para aumentar la cantidad vendida debe reducirse el precio de toda la producción por lo que el dato de ingreso marginal es anecdótico.Utilidad Marginal es el aumento o disminución de la utilidad total que acompaña el aumento o disminución de la cantidad que se posee de un Bien. Un ejemplo que lo ilustra es el caso de ua persona sedienta que encuentra un vaso de agua en el desierto. El primer vaso será extremadamente valorado. Pero si se toma un segundo vaso dicha valoración va a ser menor. El vaso numero 10 probablemente no le generará ningún placer, pudiendo ocasionar incluso un malestar.
La propensión marginal al consumo se define como el aumento del consumo con la renta disponible, matemáticamente puede expresarse como la siguiente derivada:
Que explica cuánto varía el consumo cuando varía el ingreso. En el análisis de consumo keynesiano, se formula la siguiente expresión de consumo:
Que se considera aproximadamente válida para intervalos de variación de la renta en los que la PMC permanece aproximadamente constante:
= Consumo
= Consumo autónomo o fijo.
= Propensión marginal a consumir
= Ingreso disponible
= Propensión marginal a ahorrar.
La propensión marginal al ahorro se define partir de la propensión marginal a consumir. Matemáticamente puede expresarse como la siguiente derivada:
que explica cuánto varía el consumo cuando varía el ingreso. En el análisis de consumo keynesianismo, se formula la siguiente expresión de consumo:
Que se considera aproximademente válida para intervalos de variación de la renta en los que la PMC permanece aproximadamente constante:
= Consumo
= Consumo autónomo o fijo.
= Propensión marginal al consumo
= Ingreso disponible
= Propensión marginal a ahorrar.
Conclusión Unidad 3:La importancia que tiene al estudiar derivados y límites, nos permite conocer cómo se ejecuta todos sus pasos; La derivada se aplica en los casos donde es necesario medir la rapidez con que se produce el cambio de una situación. La derivación constituye una de las operaciones de mayor importancia cuando tratamos de funciones reales de variable real puesto que nos indica la tasa de variación de la función en un instante determinado o para un valor determinado de la variable, si ésta no es el tiempo. Al igual, la derivada de una función para un valor de la variable es la tasa de variación instantánea de dicha función y para el valor concreto de la variable.
- Unidad IV. Tópicos complementarios de diferenciación.
- OBJETIVO:
- El alumno aprenderá el uso de técnicas avanzadas de derivación y susaplicaciones, para casos especiales como derivadas de funciones exponenciales,funciones logarítmicas y funciones implícitas, entre otras. Comprenderá elconcepto de diferencial y sus aplicaciones.
4.1. Derivadas de funciones logarítmicas.
- La derivada
de un logaritmo en base a es igual a la derivada de la función
dividida por la función, y por el logaritmo en base a de e.
Como, también se puede expresar así:
4.2. Derivadas de funciones exponenciales.
La derivada de la función exponencial ea igual a la misma función por el logaritmo neperiano de la base y por la derivada del exponente.Derivada de la función exponencial de base eLa derivada de la función exponencial de base e ea igual a la misma función por la derivada del exponente.
4.3 Diferenciación implícita.
- Si
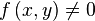 es una función implícita,
es una función implícita, - se tiene que:

4.4 Diferenciación logarítmica.- .

- .

- .

- .


- Con determinadas funciones, especialmente para
la función potencial-exponencial, es aconsejable el
empleo de la derivación
logarítmica, ya que
facilitan bastante el cálculo.
4.5 Derivadas de orden superior."Sacar todas las derivadas posibles"f(x) = 4x³+8x²+6xf(x) = 12x² + 16x +6f(x) = 24x +16f(x) = 24
4.6 Diferenciales.El diferencial es un objeto matemático que representa la parte principal del cambio en la linealización de una función y = ƒ(x) con respecto a cambios en la variable independiente.Informalmente, el diferencial dy se define en cursos introductorios mediante la expresión:
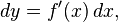 donde
donde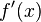 es la derivada de f con respecto a x, y donde dx es una variable real adicional (de manera que dy es una función de dos variables x, y dx). La notación es tal que la expresión:
es la derivada de f con respecto a x, y donde dx es una variable real adicional (de manera que dy es una función de dos variables x, y dx). La notación es tal que la expresión:
donde la derivada es representada en la notación de Leibniz dy/dx, se mantiene, y es consistente con respecto a la derivada como el cociente de diferenciales.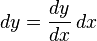
CONCLUSIÓN FINAL UNIDAD IVLa interpretación de la derivada como la pendiente de la recta tangente proporciona información acerca del comportamiento de las funciones, lo cual resulta muy útil para trazar su grafica. La recta tangente en un punto proporciona una aproximación lineal al comportamiento de la función en un entorno o vecindad del punto. Las tangentes a una curva son también extremadamente útiles al analizar donde crece, donde decrece una función y donde se sitúan sus valores máximos y mínimos. Estos temas serán discutidos en esta unidad.
Unidad V. Aplicaciones de la
derivada.OBJETIVO:El alumno analizará el comportamiento de las funciones con el uso de técnicas de
optimización. Aplicará estas técnicas en la resolución de problemas de las
disciplinas económico-administrativas.5.1 Función creciente y decreciente.
Una función f es creciente es un intervalo si para cualquier par de números x1,x2 del intervalo. .
.
Una fución f es decreciente es un intervalo si para cualquier par de números x1,x2 del intervalo, .
.
Sea f una función continua con ecuación y = f(x), definida en un intervalo [a,b]. La siguiente es la representación gráfica de f en el intervalo[a,b]. En la gráfica anterior puede observarse que la función f es:
En la gráfica anterior puede observarse que la función f es:
1.) Creciente en los intervalos (a,x3),(x5,x6)
2.) Decreciente en los intervalos(x3,x5),(x6,b)
Criterio de crecimiento y decrecimiento
Sea f una función continua en el intervalo cerrado![\left [ a,b\right ]](http://www.wikimatematica.org/images/math/f/9/4/f944498af9d6490b5599ba93146f9db8.png) y derivable en el intervalo abierto
y derivable en el intervalo abierto  .
.
- Si
 es creciente en
es creciente en ![\left [ a,b \right ]](http://www.wikimatematica.org/images/math/f/9/4/f944498af9d6490b5599ba93146f9db8.png)
- Si
 es decreciente en
es decreciente en ![\left [ a,b \right ]](http://www.wikimatematica.org/images/math/f/9/4/f944498af9d6490b5599ba93146f9db8.png)
- Si
 es constante en
es constante en ![\left [ a,b \right ]](http://www.wikimatematica.org/images/math/f/9/4/f944498af9d6490b5599ba93146f9db8.png)
Ejemplo 1
Determinemos los intervalos en que crece o decrece la función con ecuación f(x) = 1 / 2(x2 − 4x + 1).
Para ello calculemos la primera derivada de f:f'(x) = x − 2.
Como f'(x) > 0 ↔ x − 2 > 0, o sea si x > 2, entonces f es creciente para x > 2.
Como f'(x) < 0 ↔ x − 2 < 0, o sea si x < 2, entonces f es decreciente para x < 2.
En la gráfica de la función puede observarse lo obtenido anteriormente.
5.2 Extremos relativos y extremos absolutos.El "Máximo Relativo" se da cuanto tienes un cambio de signo en la pendiente de la recta tangente de la curva.
La fórmula de cálculo es muy sencilla. Tienes que derivar a la función y observar en que puntos la derivada primera se iguala a cero. O sea:
Partiendo de f(x)
Obtienes f´(x)
La igualas a 0, f´(x)=0
Con lo que obtendrás una serie de valores de x que satisfacen la ecuación. Estos valores de x los remplazas en la ecuación original y obtendrás las coordenadas de los posibles máximos y mínimos. Para saber si son relativos o absolutos debes compararlos entre si.
https://es.answers.yahoo.com/question/index;_ylt=A0SO81zYymBVXXMA5TXD8Qt.;_ylu=X3oDMTBya2cwZmh2BGNvbG8DZ3ExBHBvcwM1BHZ0aWQDBHNlYwNzcg--?qid=2009032
9053259AAivbHn
5.3. Prueba de la primera derivada para la determinación de máximos y mínimos.
Se llama Criterio de la primera derivada al método o teorema utilizado frecuentemente en el cálculo matemático para determinar los mínimos y máximos relativos que pueden existir en una función mediante el uso de la primera derivada o derivada principal, donde se observa el cambio de signo, en un intervalo abierto señalado que contiene al punto crítico.
Seaun punto crítico de una función
que es continua en un intervalo abierto
que contiene a
. Si
es derivable en el intervalo, excepto posiblemente en
, entonces
puede clasificarse como sigue."
1. Si
'
cambia de positiva a negativa en
, entonces
tiene un máximo relativo en
.
2. Si
'
cambia de negativa a positiva en
, entonces
tiene un mínimo relativo en
.
3. Si
'
es positiva en ambos lados de
o negativa en ambos lados de c, entonces
no es ni un mínimo ni un máximo relativo.
http://es.wikipedia.org/wiki/Criterio_de_la_primera_derivada
5.4 Concavidad, puntos de inflexión y prueba de la segunda derivada.
CONCAVIDAD:
f presenta concavidad positiva en x=a si existe un E*a / para todo x perteneciente al E*af(x) > f'(a)(x-a) + f(a). 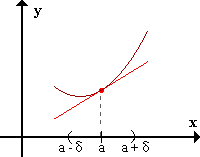
La función presenta concavidad positiva en el punto a si, en un entorno reducido de a, la gráfica de f está "por encima" de la recta tangente a f(x) en el punto a. f presenta concavidad negativa en x=a si existe un E*a / para todo x perteneciente al E*af(x) < f'(a)(x-a) + f(a). f presenta concavidad negativa en x=a si existe un E*a / para todo x perteneciente al E*af(x) < f'(a)(x-a) + f(a). 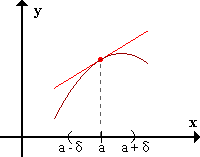
La función presenta concavidad negativa en el punto a si, en un entorno reducido de a, la gráfica de f está "por debajo" de la recta tangente a f(x) en el punto a.
PUNTOS DE INFLEXIÓN:
f presenta un punto de inflexión en x=a si existeδ > 0 / para todo x perteneciente a(a - δ,a) f(x) > f'(a)(x-a) + f(a) y para todo x perteneciente a(a,a + δ) f(x) < f'(a)(x-a) + f(a) (o viceversa: f menor a la izquierda y mayor a la derecha).
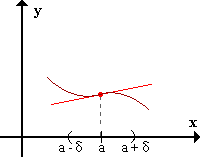
En el semientorno izquierdo de a, f está por encima de la tangente a f(x) en a, y en el semientorno derecho de a, f está por debajo de la tangente. 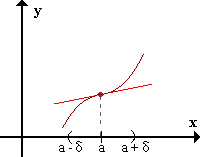
En el semientorno izquierdo de a, f está por debajo de la tangente a f(x) en a, y en el semientorno derecho de a, f está por encima de la tangente.
SEGUNDA DERIVADA:
Suponga f' de a es = 0, si f'' (a) es menor que 0, entonces f tiene un maximo relativo en a.
Si f'' (a) es mayor que 0, entonces f tiene un minimo relativo en a.
5.5. Optimización de funciones económico-administrativas: maximización de funciones de ingreso, utilidad y beneficios; minimización de funciones de costos y costos promedio.
MAXIMOS Y MINIMOS1. (UTILIDAD MAXIMA) Una empresa vende todas las unidades producidas a $4.00 cada una. El gasto total de la empresa G por producir x unidades esta dado en dólares por
G=50+1.3x+0.001x²
a) Escriba la expresión para la utilidad total P como una función x.
b) Determine el volumen de producción x de modo que la utilidad P sea máxima.
c) ¿Cuál es el valor de la utilidad máxima?
P=4
C=50+1.3x+0.001x²
A) P=4x-50-1.3x-0.001x²≠
P=2.7x-50-0.001x²
P'(x)=0.002x-2.7
2.7
0.002
=x
B) x=1350≠
P=2.7 (1350)-0.001(1350)2 -50
C) P=1,772.50 ≠
2. (Costo promedio mínimo) El costo promedio de fabricar cierto artículo es
C=5+48x+3x2
En donde x es el número de artículos producidos.
Encuentre el valor mínimo de C.
C=5+48x+3x2
C=5+48x-1+3x2
C'=48x2+6x
O=6x- 48x2
6x(x2)=48
x3= 486
X=2 ≠
C=5+482+3(2)2
C=5+482+3(4)
C=41≠
C es 41 cuando x=2
3. (Costo promedio mínimo) El costo de producir x artículos de cierto producto es:
C (x) =4000+3x+10-3x2
Determine el valor de x que hace del costo promedio por artículo un mínimo.
C(x)=4000+3x+0.001x2
Cx=4000x+ 3xx+ 0.001x2x
C(x)=4000x-1+3+0.001x
C'x=-4000x-2+0.001
C'(x)=-4000x2+0.001
-4000x2+0.001=0
-0.001(x2)=4000
0.001(x2)=4000
x= 210000.001
x= 2000
4. (Utilidad máxima) En el ejercicio anterior, los artículos en cuestión se venden a $8.00 cada uno. Encuentre el valor de x que maximiza la utilidad y calcule la utilidad máxima.
C(x)=4000+3x+0.001x2
I=8x
G=8x - 4000-3x - 0.001x2
G=5x – 4000 - 0.001x2
G'=5 - 0.002x
50.002=x
X=2500
G=5(2500) – 4000 – 0.001 (2500)2
=12500 – 4000 – 6250
G=2250http://www.buenastareas.com/ensayos/Aplicacion-De-Maximos-y-Minimos/313571.html
5.6 Elasticidades: elasticidad de la demanda y elasticidad del ingreso.
DEMANDA:
¿Que tanto puede variar el preco sin que afecte la demanda?
Si P= fq es una funcón de demanda difernciable, la elasticidad puntual de la demanda, denotada por la letra n, en (P,q) está dada por
=n (q) = p
-----
q
------------
dp
-------
dq
NOTA:
Cuando el valor absoluto de n es mayor que uno la demanda en elastica.
InI >1
Cuando el valor absoluto de n es = 1 es elaticidad unitaria
InI = 1
Cuando el valor absoluto es menor que 1 es inelastica
InI < 1
ELASTICIDAD:
r=pq
u=P u' =dq
-------
dp
V= q v'= 1
r'= P+ dq
------ . q
dp
r'= P(1+ dq q )
----- . ------
dp p
dr
----- = P (1 + 1)
dq ----
n
Conclusión Unidad 5.
La derivada tiene una gran variedad de aplicaciones además de darnos la pendiente de la tangente a una curva en un punto. Se puede usar la derivada para estudiar tasas de variación, valores máximos y mínimos de una función, concavidad y convexidad, etc.Familiarizarse con el cálculo automático de derivadas, con la regla de la cadena para la derivación de funciones compuestas, con la derivación múltiple y —finalmente— con la derivación implícita.
CONCLUSIÓN GENERAL:
Cada uno de los temas presentados, dan la oportunidad de conocer un poco más a fondo, sobre las funciones, limites, derivadas, etc, para asi tener un mejor aprendizaje, espero que este blog sirva de mucha ayuda para quienes quieran conocer más de lleno cada uno de estos temas, que son de suma importancia.
- Si